では実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。 練習1 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1 概形と底面は下の図のようになる。底面積を求めて $$\pi \times 3^2=9\pi$$ 体積の公式に当てはめて $$9\pi \times 4 \times \frac{1}{3}$$ $$=12\pi cm^3$$ となります。 半径がわからない場合でも 考え方は、高さを求めるときと同じですね! 円錐の体積を求める方法 まとめ お疲れ様でした! 円錐の体積を角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ※ このQ&Aでは、 「進研ゼミ

角錐 円錐の体積 Youtube
円錐 体積 求め方
円錐 体積 求め方-円錐の体積は、底面積×高さ×3分の1です。 円錐の表面積は、展開して扇形と円になるので、計算して足せばいいです。 扇形の面積の出し方は、 面積=2分の1×弧の長さ×半径です。円錐の体積と公式の問題、高さの求め方 下図の円錐の体積を、公式を用いて求めましょう。 上記の値を公式に当てはめれば良いので簡単ですね。 また下図の円錐の体積=15m 3 、半径=2mのとき、高さを求めてください。 円錐の高さは下式を用いて算定し



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
でしたら、今からお教えする解き方を きちんとマスターしておきましょう! まずは公式です。 これは必須事項ですので 必ず! 覚えるようにしてください。 円錐の体積 =(底面積)×(高さ)× 1/3 では、この公式を実際に 当てはめてみましょう!円錐の体積の公式を用いた場合 円錐の体積の公式より, V = 1 3 π r 2 h = 1 3 π × 1 2 × 1 = π 3 定積分の公式を用いた場合 定積分の基本式より, ∫ a b f (x) d x = F (x) a b = F (b) − F (a) ( F (x) は f (x) の原始関数の1である ) 求める円錐の底面積 S (x) を S (x) = π {f③錐体の体積の求め方の根本を考える ④体積を拡縮してみる ①特別な四角錐を考える 底面積が一辺 の正方形,高さが の四角錐を考える. これを6つ組み合わせる. この立方体の体積= 1つの四角錐の体積は次式で表される. 四角錐の体積= →「底面積×
Q 台形の体積 台形の体積の求め方を教えて下さい。 底面積(a1×a2)、上面積(b1×b2)、高さh、勾配11とする場合の体積の求め方。 勾配が変わった場合はどうなるのか。 また、オペリスク公式とは何か教えてください例 3 65 (円錐の体積) 底面の半径 ,高さ の円錐の体積は である. これを多重積分で求める. 円錐の底面は 平面にあるとし, その領域を図の円すいの体積を求めなさい。 問題の見方 立体の体積を求める公式より,~~すいとつく立体の場合, $$(底面積)×(高さ)×\frac{1}{3}=(体積)$$ で求められます。~~すいの立体のときは,$$\frac{1}{3}$$をかけ算するのがポイントです。
相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね! それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの③錐体の体積の求め方の根本を考える ④体積を拡縮してみる ①特別な四角錐を考える 底面積が一辺 の正方形,高さが の四角錐を考える. これを6つ組み合わせる. この立方体の体積= 1つの四角錐の体積は次式で表される. 四角錐の体積= →「底面積×次の章では、学校で学習する円錐の基本的な考え方について解説していくよ! 簡単なやり方だけでなく、基本的な考え方も身につけておけると数学の基礎力向上にもつながってきます。 がんばって理解していきましょう♪ スポンサーリンク



斜軸回転体の体積 応用編 ド モアブルの定理利用 おいしい数学



壮大 台形 体積 求め 方 壁紙 配布
底面積を求めて $$\pi \times 3^2=9\pi$$ 体積の公式に当てはめて $$9\pi \times 4 \times \frac{1}{3}$$ $$=12\pi cm^3$$ となります。 半径がわからない場合でも 考え方は、高さを求めるときと同じですね! 円錐の体積を求める方法 まとめ お疲れ様でした! 円錐の体積を円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体円柱・円錐の体積の求め方 円柱の体積の求め方を覚えるにあたって、基本となるのが円の面積です。 s=πr2 この円の面積は、円柱の底面積となり、あとはそれに円柱の高さをかければいいので v=πr2h が円柱の体積の求め方となります。



円錐の体積を求める Youtube



中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室
円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただしでは実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。 練習1 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1 概形と底面は下の図のようになる。円錐の体積を求める公式は、 V = 1/3 Sh = 1/3 πr^2 h で表されます。 このページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。



中3 三角形の相似 円錐の体積比 日本語版 Youtube



円錐台 Wikipedia
円錐の体積=底面積×高さ÷3 円錐の底面積は円の面積ですので、円の面積×高さ÷3で求めることができます。 ⇒ 円の面積の求め方 スポンサードリンク 円錐の体積を求める問題 // では、実際に円錐の体積を求める問題を解いていきたいと思います。どちらの方法でも、確かに円錐の体積は \(\color{red}{V = \displaystyle \frac{1}{3}\pi r^2 h}\) と計算できます。 このように、ある立体の体積は その立体をなす平面の面積の積み重ね(または回転)で求められる のですね。相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね! それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの
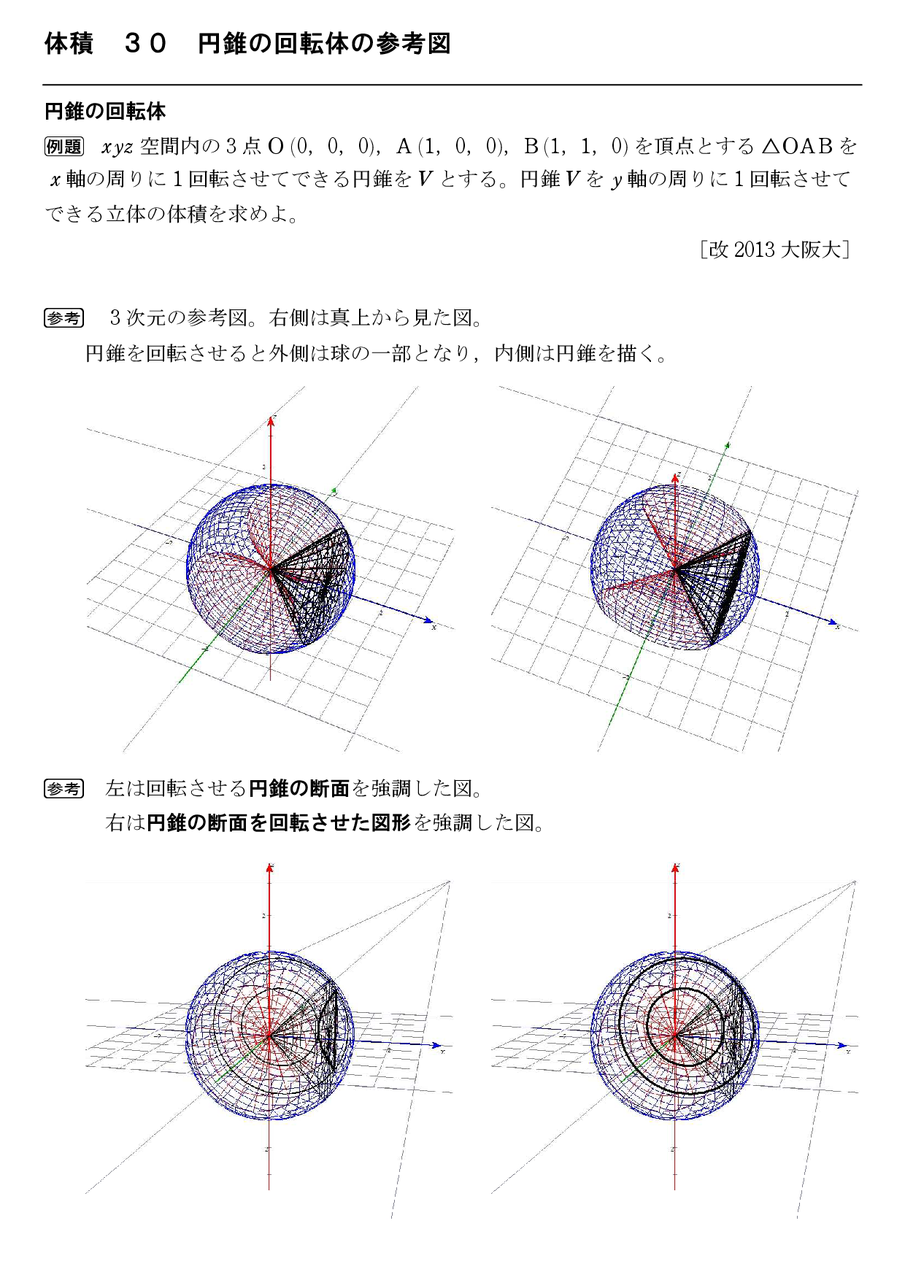


図解 円錐の回転体を図示してみよう 東大17 阪大13 理系のひとりごと



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
円錐の関連記事はこちら 中学数学円錐の体積の求め方・公式サクッと 中学数学円錐の高さの求め方頻出パターン 中学数学円錐の中心角の求め方3パターン
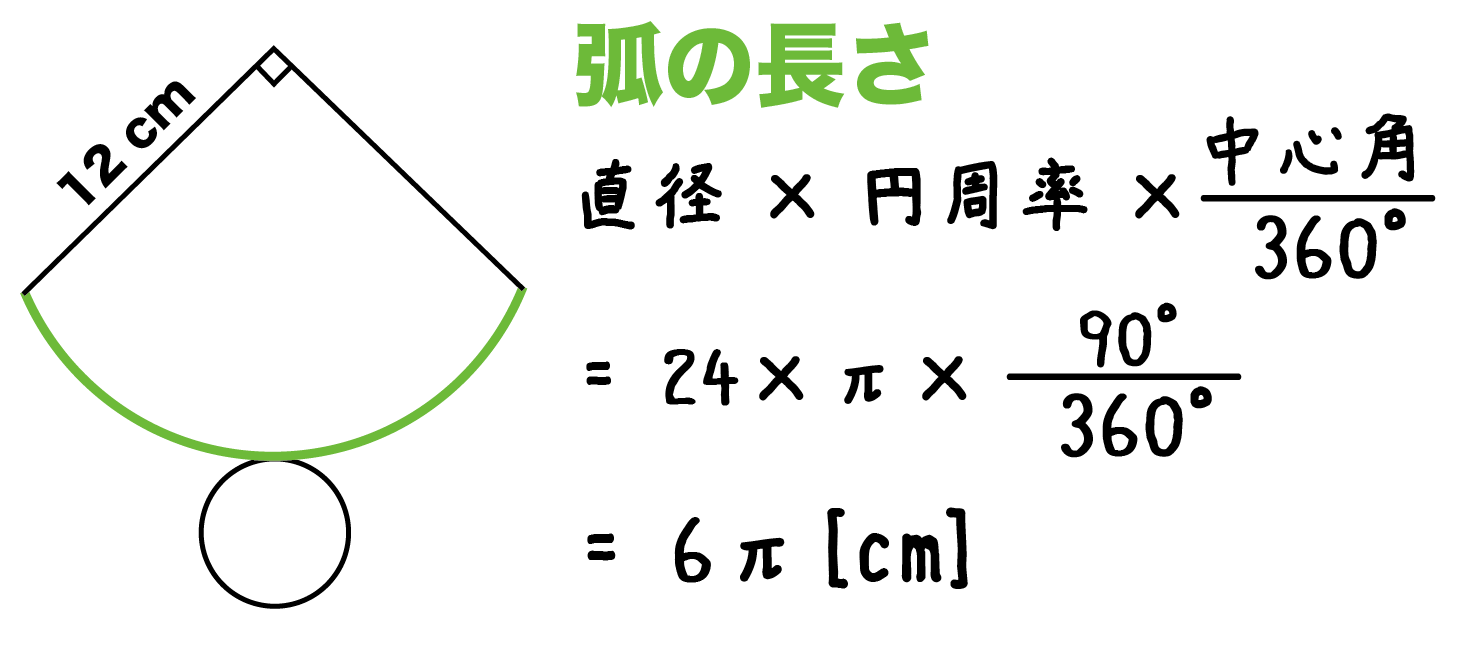


中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



中1数学 立体の体積 練習編 映像授業のtry It トライイット



数学 中学2 図形 中学数学に関する質問 勉強質問サイト



円錐の体積ってなんであの公式なの Webty Staff Blog



側面に接する曲線の長さ Okwave
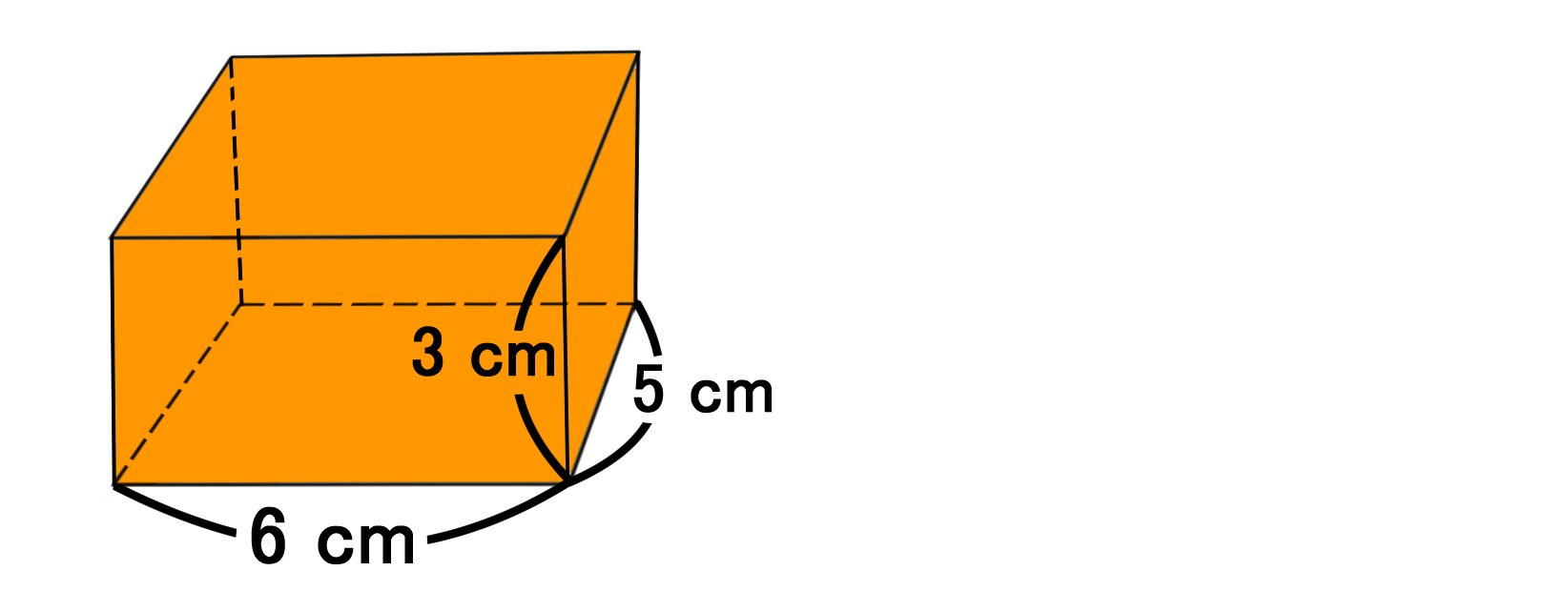


立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



テストに出る 円錐の展開図と問題 これで受験バッチリ 中学生 数学のノート Clear



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ
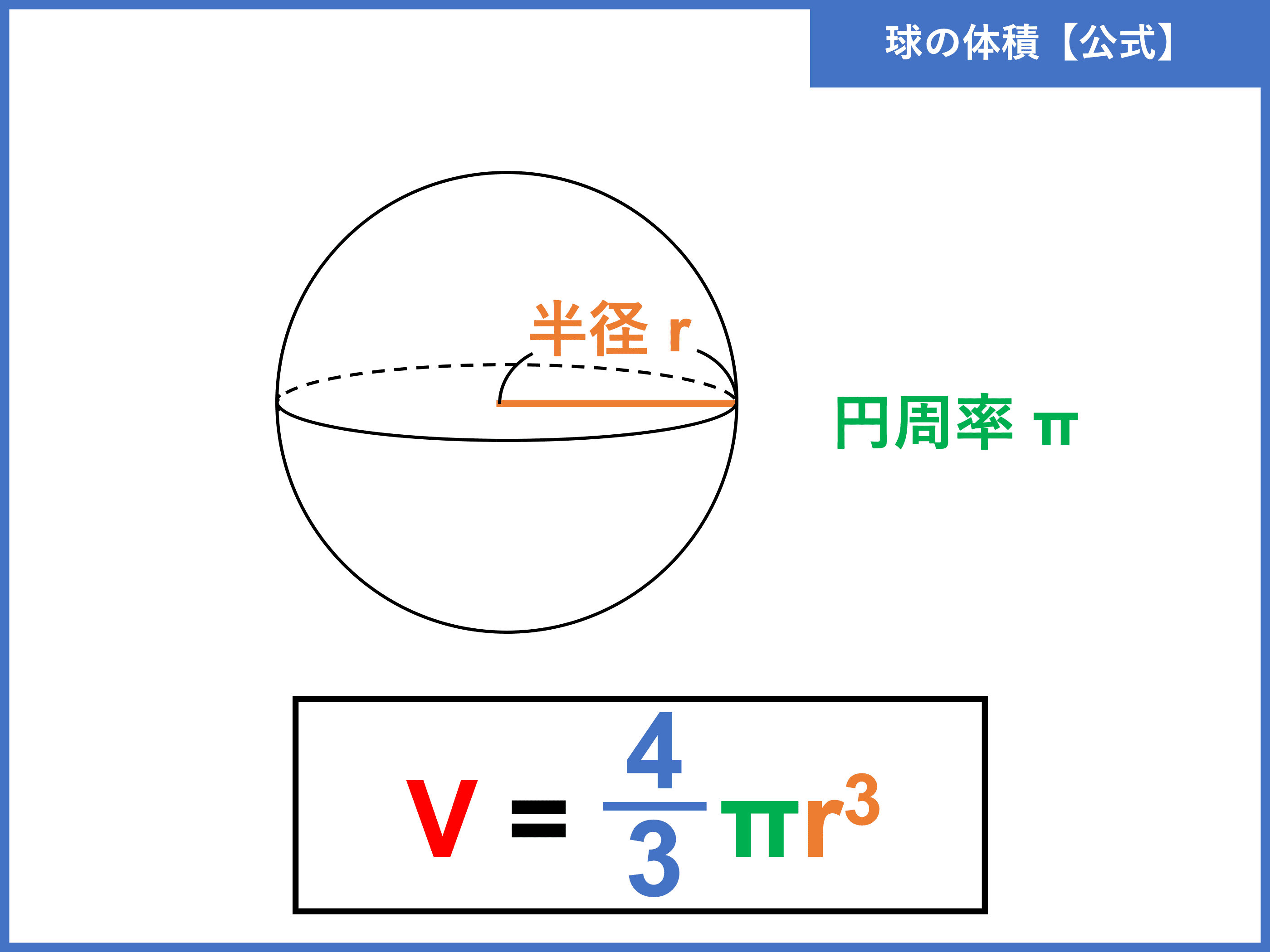


Images Of 体積 Japaneseclass Jp



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
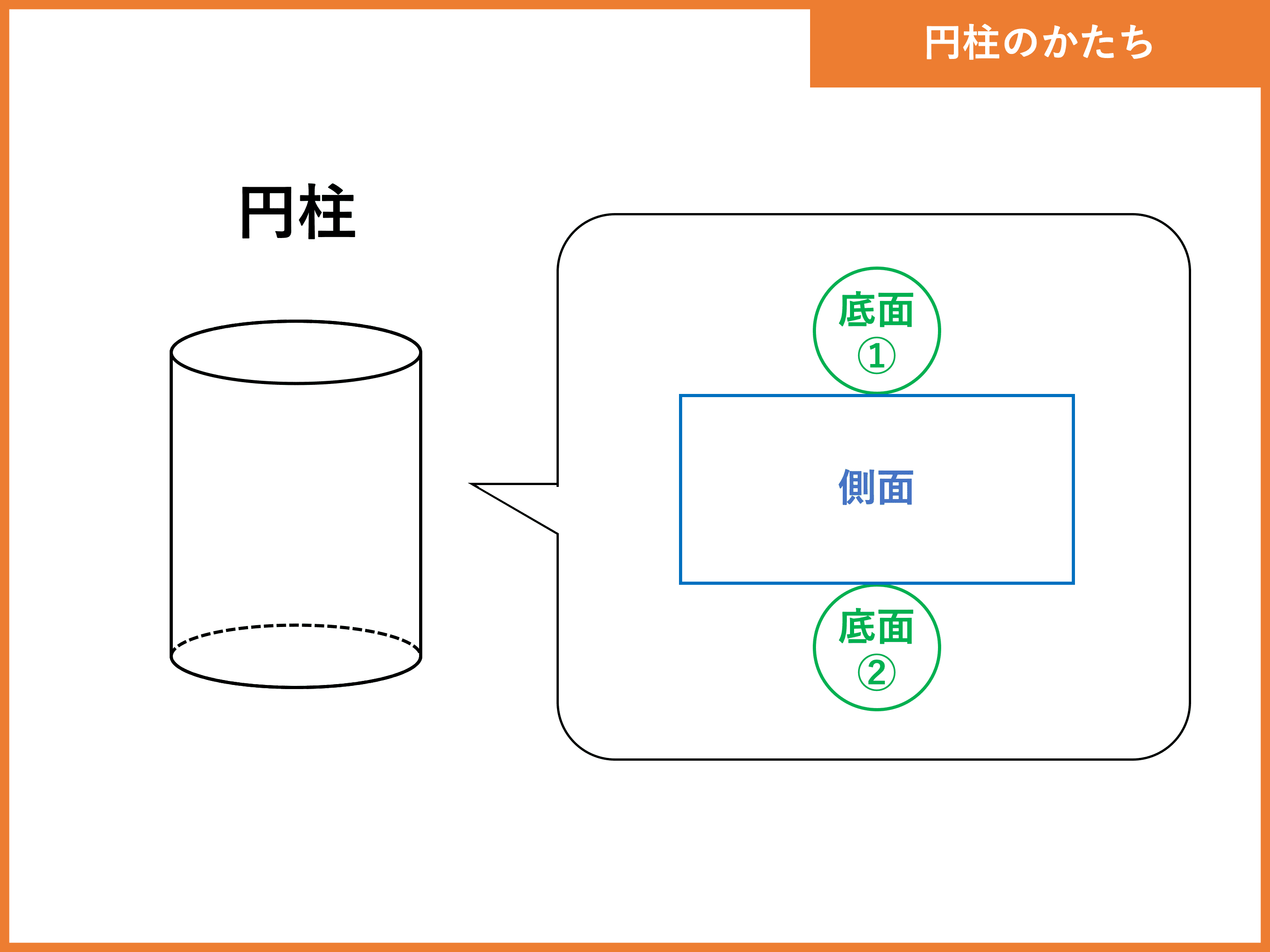


最も人気のある 円柱 表面積 公式 壁紙 配布



最高 円錐 公式 表面積 壁紙 配布



円錐の表面積 Youtube



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ


Http Www Nc Center Gsn Ed Jp Action Common Download Main Upload Id 8129
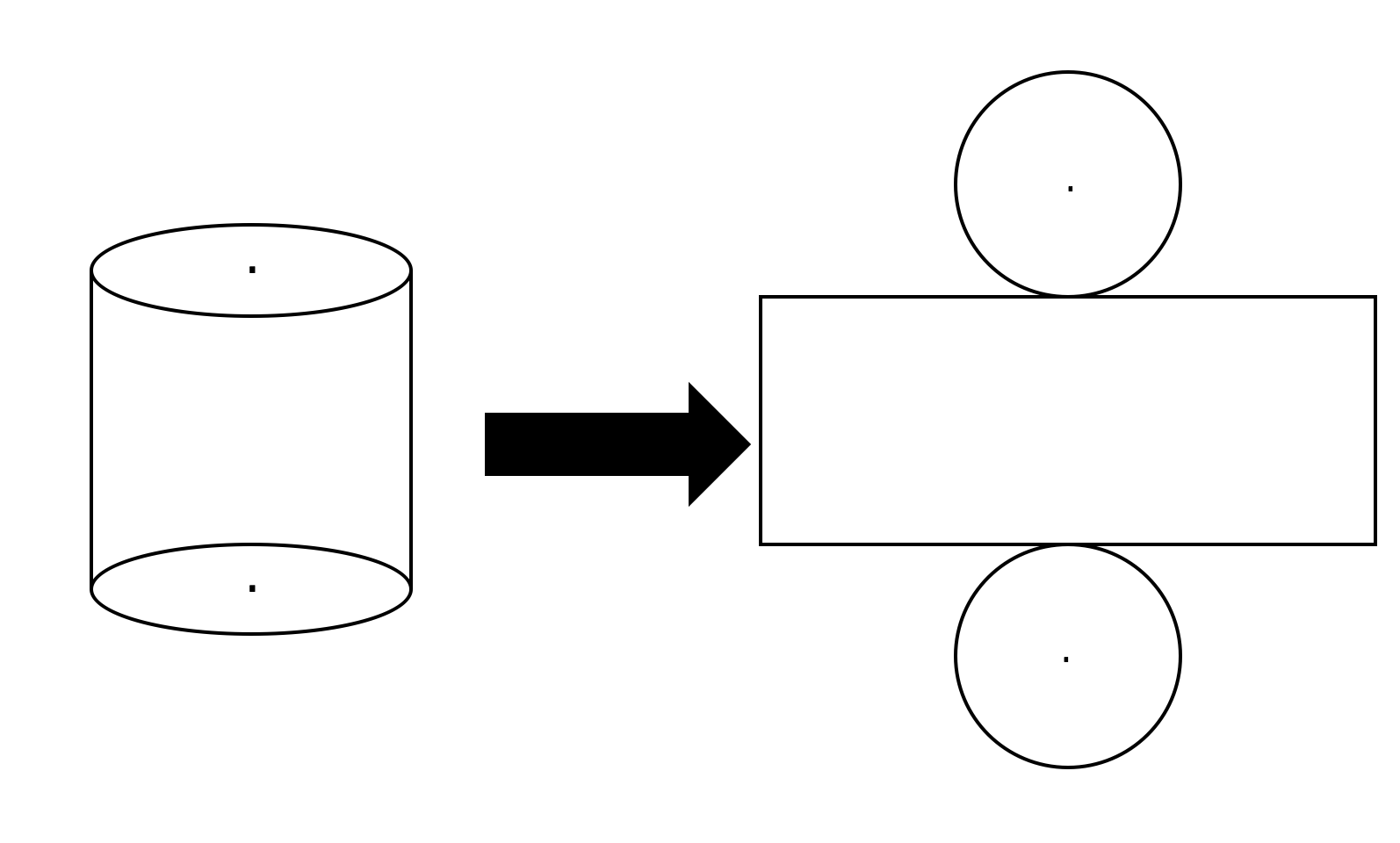


3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ



ほとんどのダウンロード 台形 の 体積 の 公式



円錐や角錐の体積の求め方 中学1年数学 Youtube
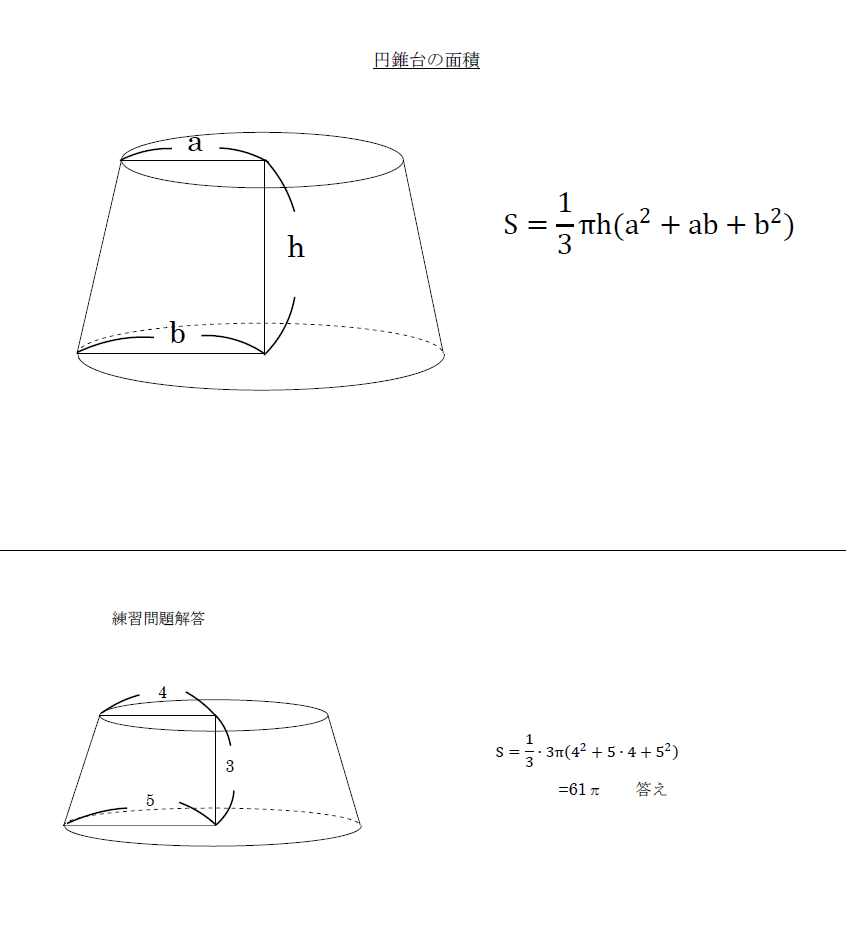


空間図形の体積 円錐台 の解法 中学 受験 定期試験 数学解き方集 裏技 解法



数 立体の体積と表面積 直前ノート 中学生 数学のノート Clear



複雑な形状の円型の管における体積の計算の仕方 Okwave



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



高校数学 立体 正四面体 直円錐 表面上の最短経路 受験の月



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく
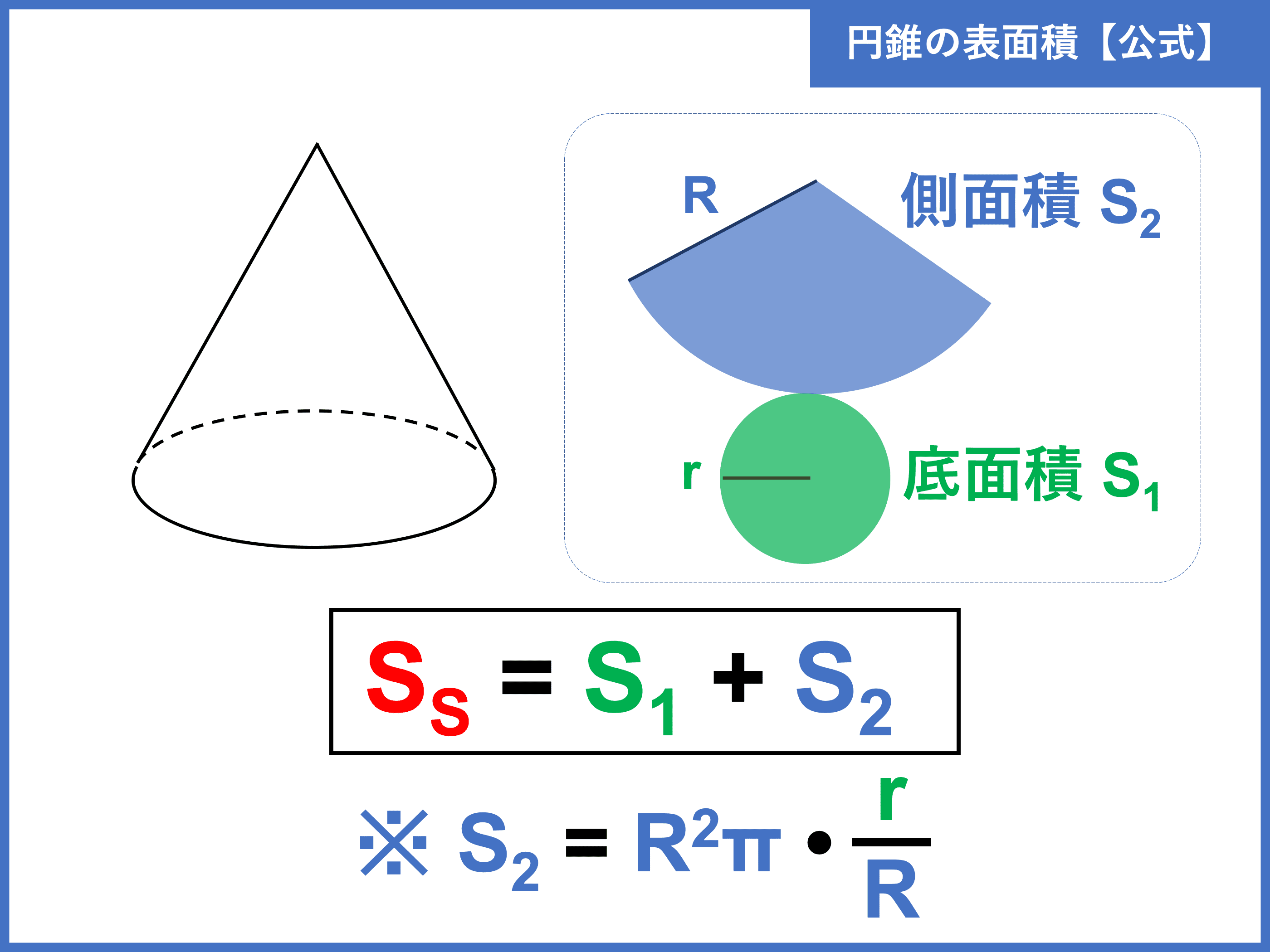


円錐とは 体積 表面積の公式や求め方 受験辞典
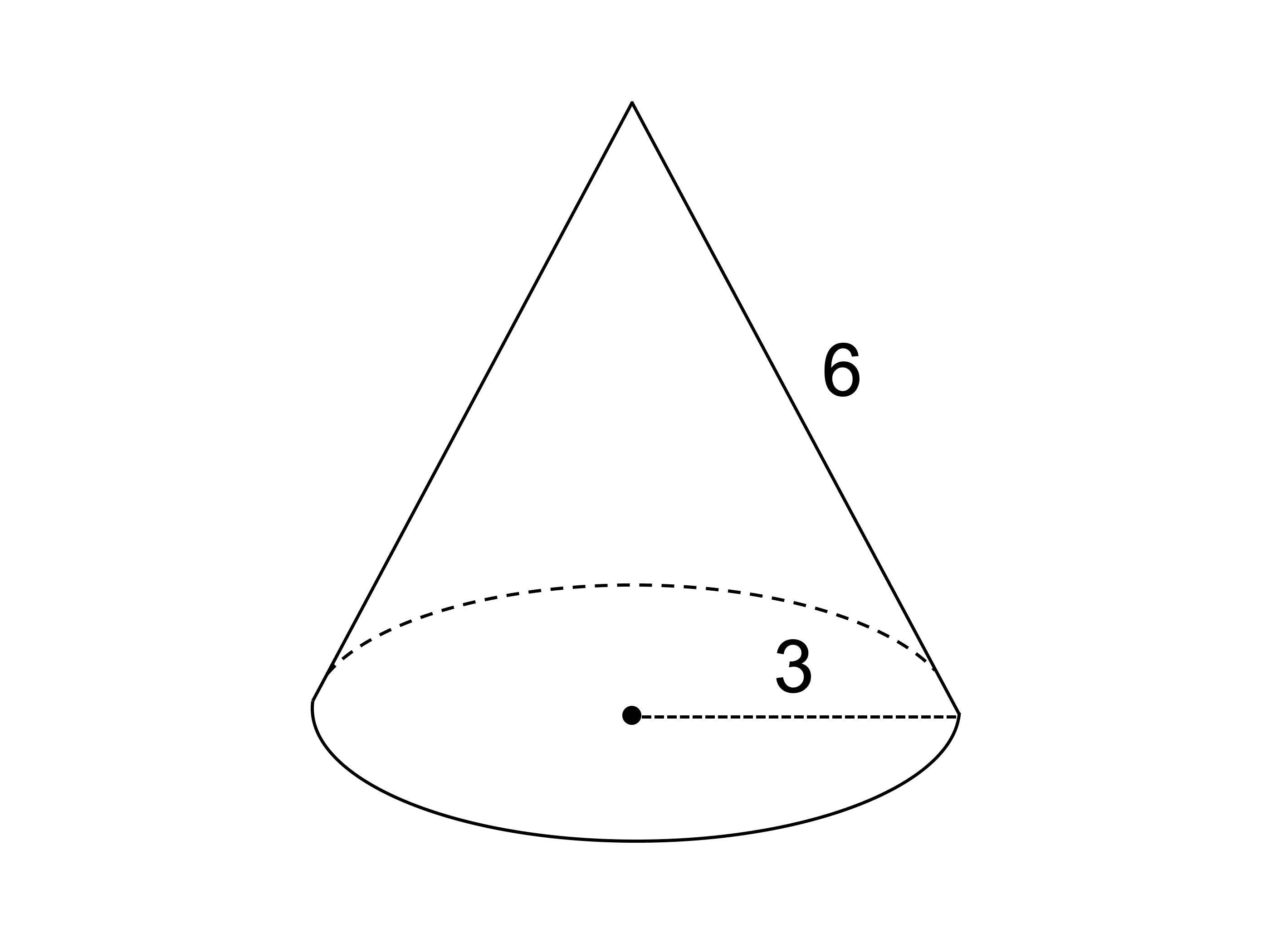


完全版 円錐の展開図の書き方 作り方 受験辞典



角錐 円錐の体積 Youtube


頭の体操 問題3 解答 Cometのサボテン栽培日記



斜軸回転体の体積 応用編 傘型積分 おいしい数学



中学2年 図形 中学数学に関する質問 勉強質問サイト



中学1年生 数学 無料問題集 角柱や円柱の体積 おかわりドリル



斜軸回転体の体積 応用編 傘型積分 おいしい数学


円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
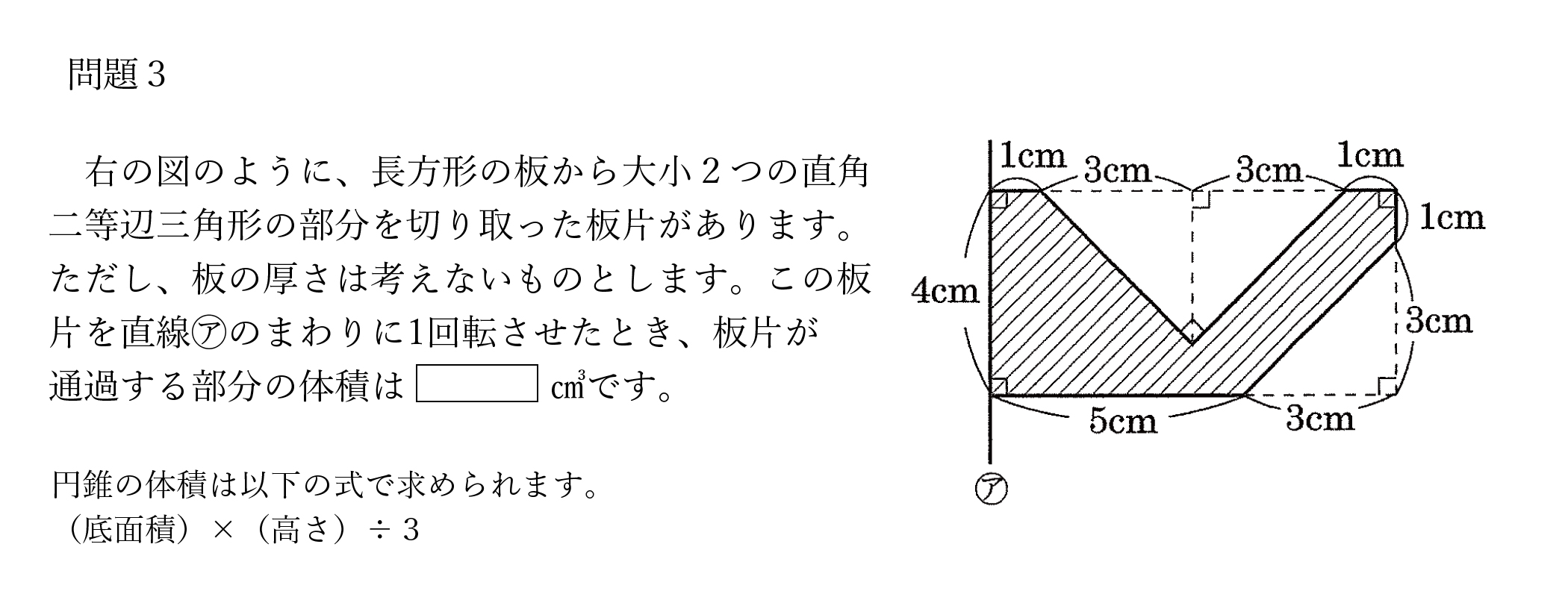


頭の体操 問題3 解答 Cometのサボテン栽培日記



どうして1 3なの 錐の体積の公式の求め方 まなべーと



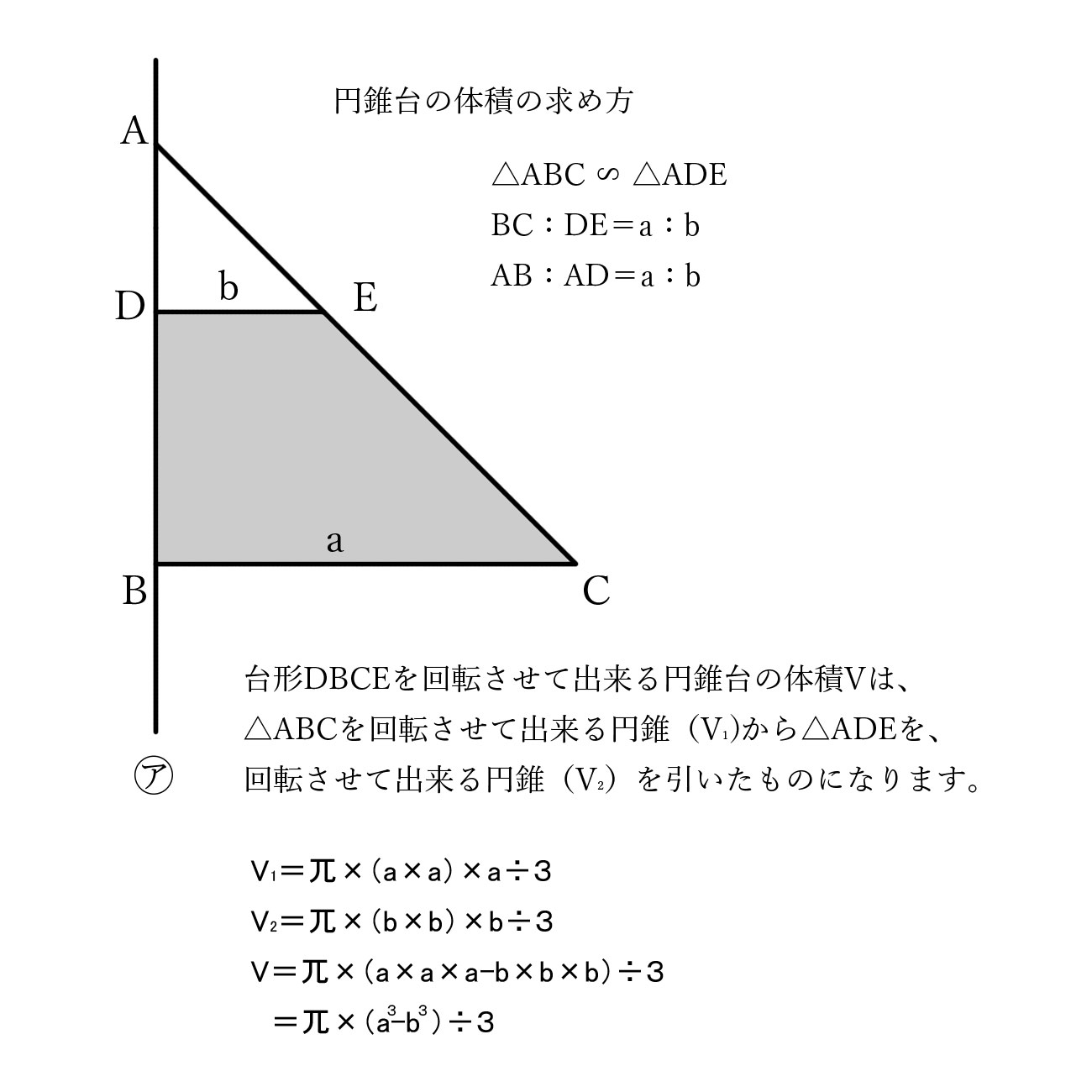
空間図形14 円すい台の体積 Youtube



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
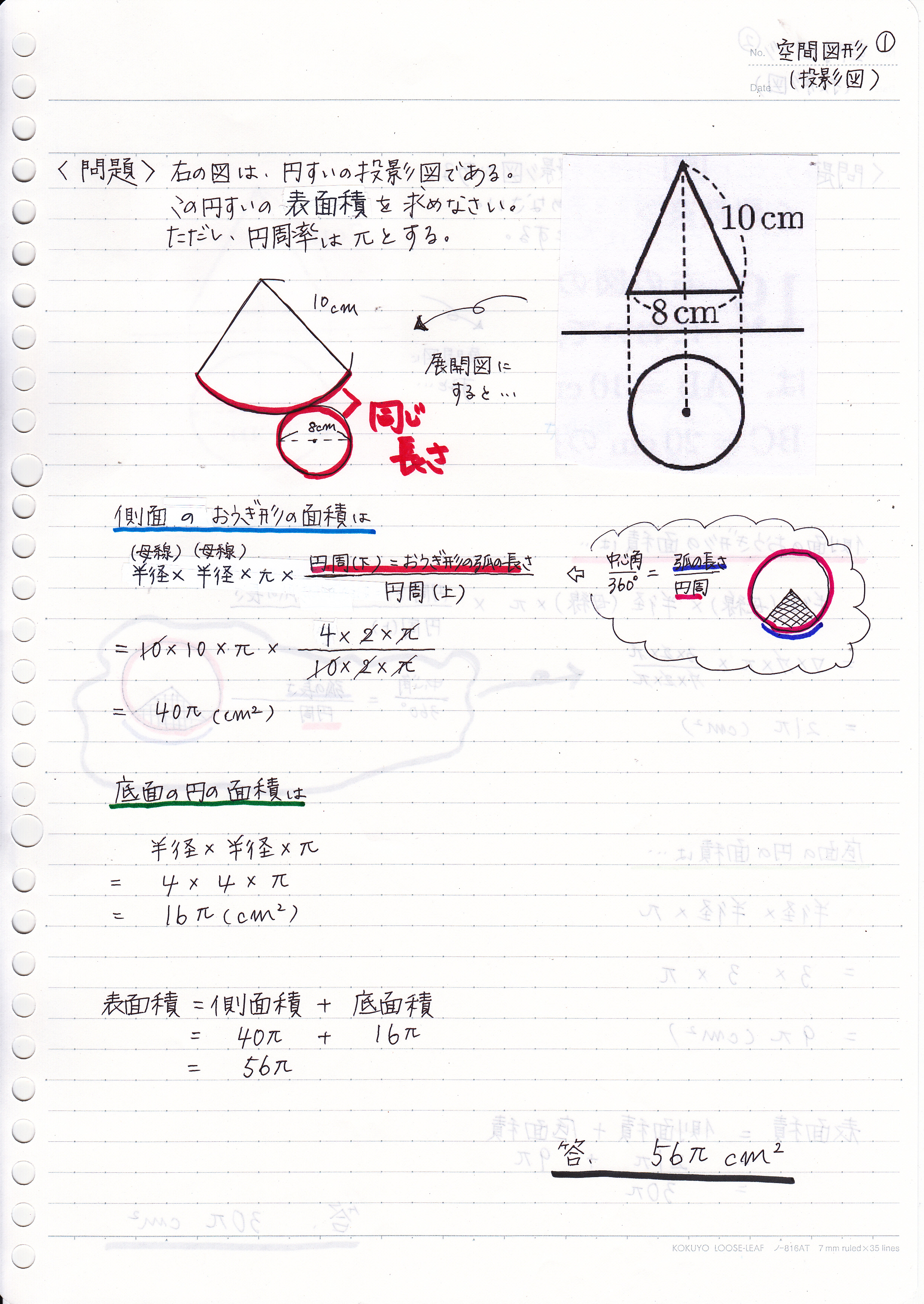


投影図から表面積を求める問題 2問 現役塾講師のわかりやすい中学数学の解き方



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく


数学だお 出雲弁でおスえぇ積分その1 標準語でも書くからねー ポンチャキー主夫の4コマ日記



中1数学 円すいの体積 表面積の求め方と練習問題 Examee



回転体 円錐の体積と表面積の求め方 現役塾講師のわかりやすい中学数学の解き方


Solidworksで入れ物の容積測定 容積計算での求め方


Http Www1 Iwate Ed Jp b H18 Hisu1801 Pdf



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ


Www Saga Ed Jp Kenkyu Kenkyu Chousa H22 04 Chu Sugaku Documents Kuukan Ikkatu Tisiki Pdf


中学数学の問題です 図の円錐を見てください 円錐の側面の展開図の X Yahoo 知恵袋


双円錐 Wikipedia


Http Www Juen Ac Jp Math Journal Files Vol27 27 169 176 Takahashi Pdf



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



立体の体積と表面積 Ict教材eboard イーボード
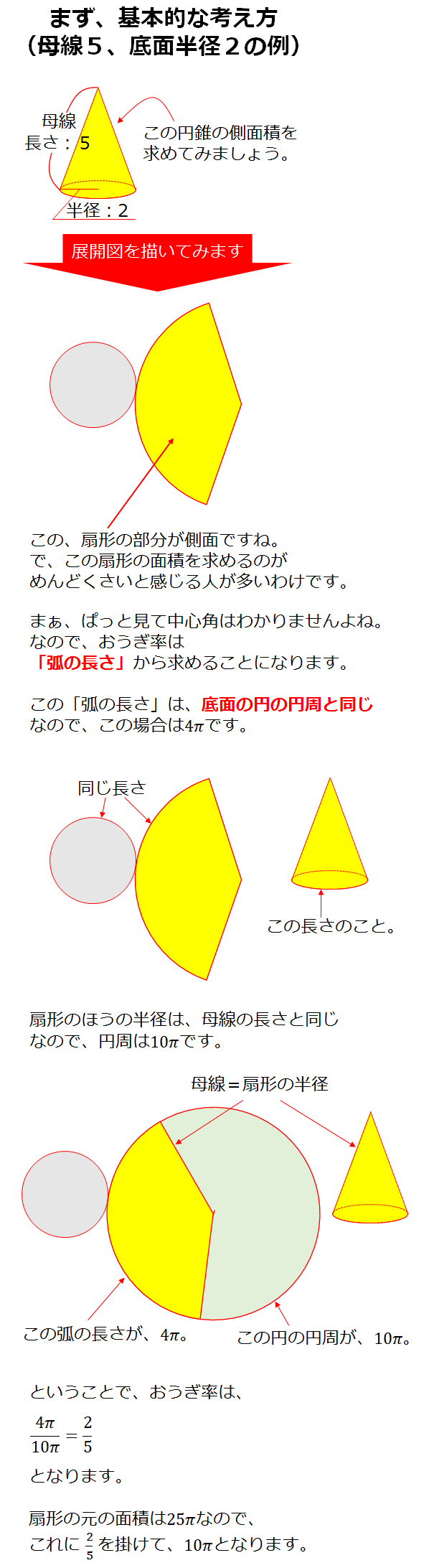


長さ 面積 体積 後編 立体 硫化鉄の 数学 を 数楽 にするブログ 楽しくドヤ顔で100点とる方法
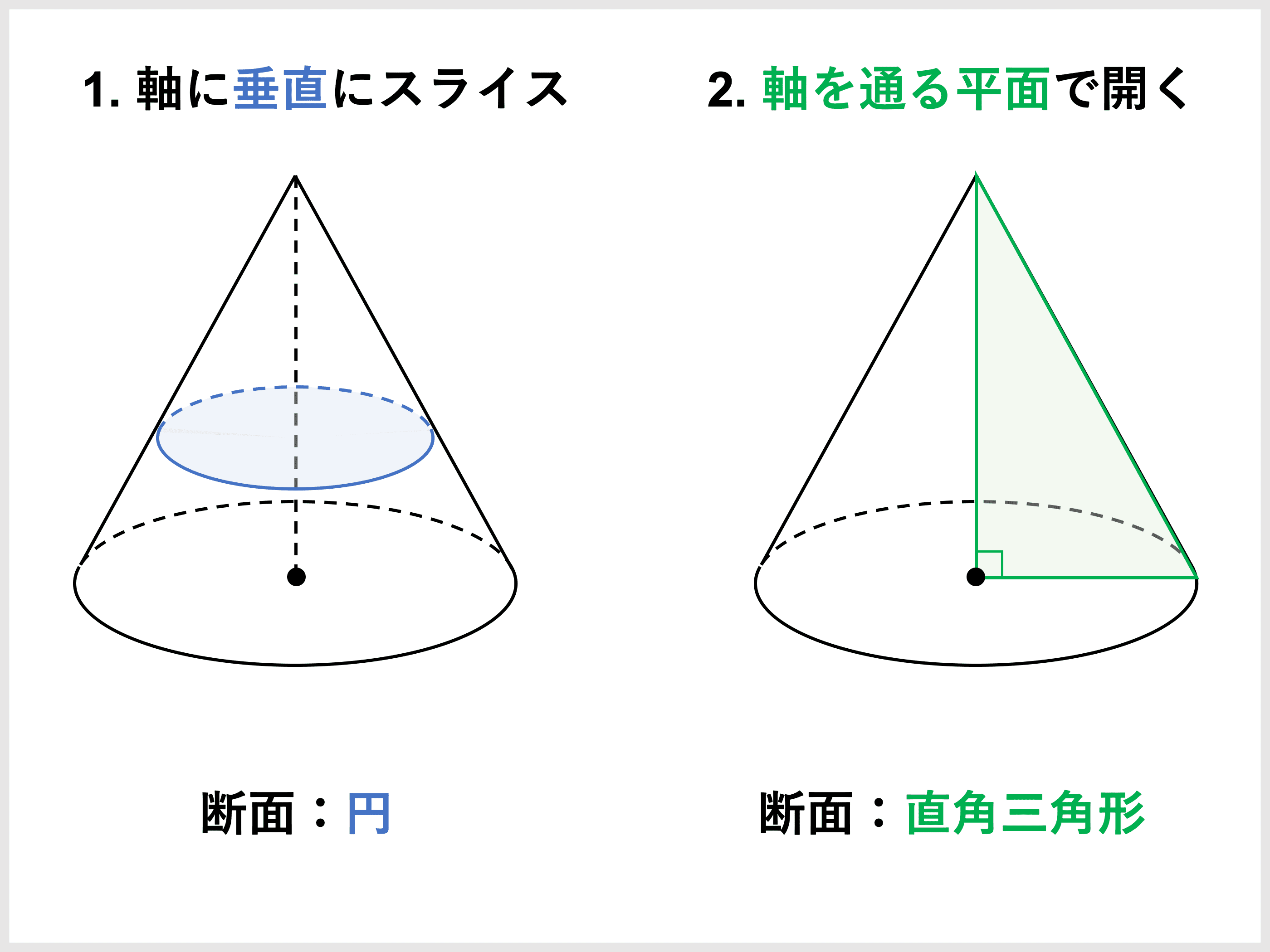


積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典
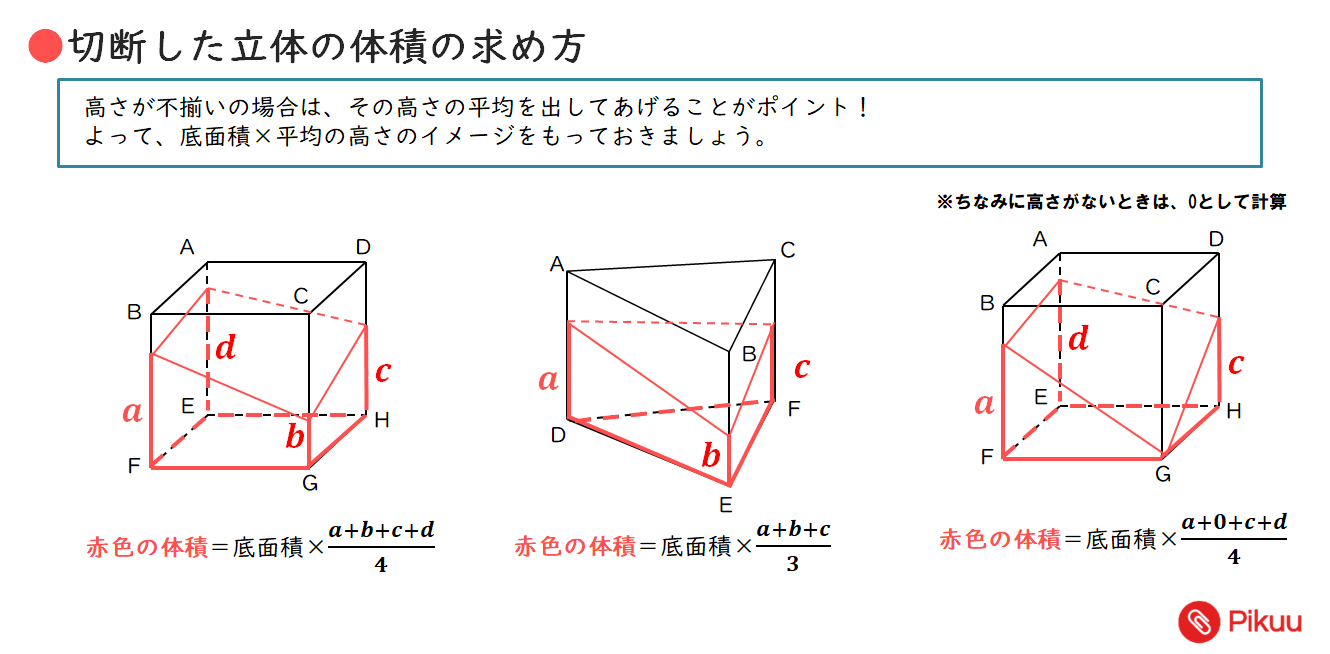


高校入試対策数学 知って得 中学数学の公式テクニック集 Pikuu
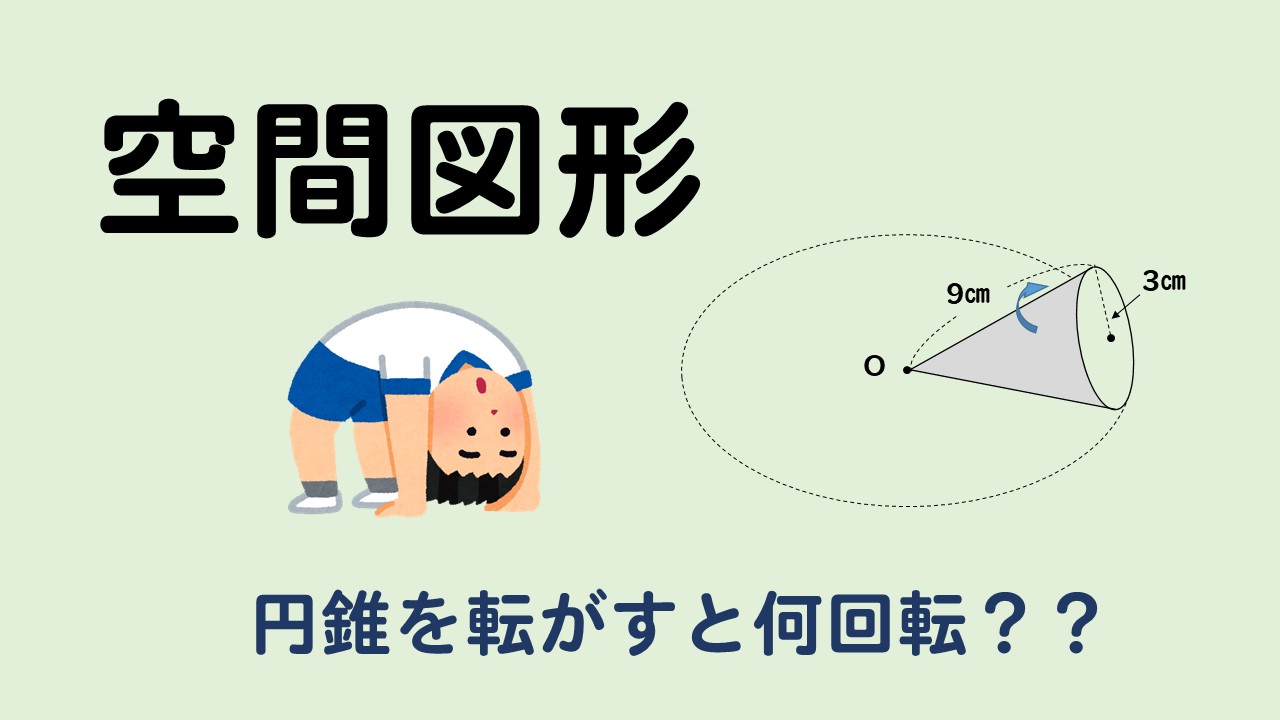


円錐を転がすと1周するのにどれくらい回転する 入試問題を解説 数スタ



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
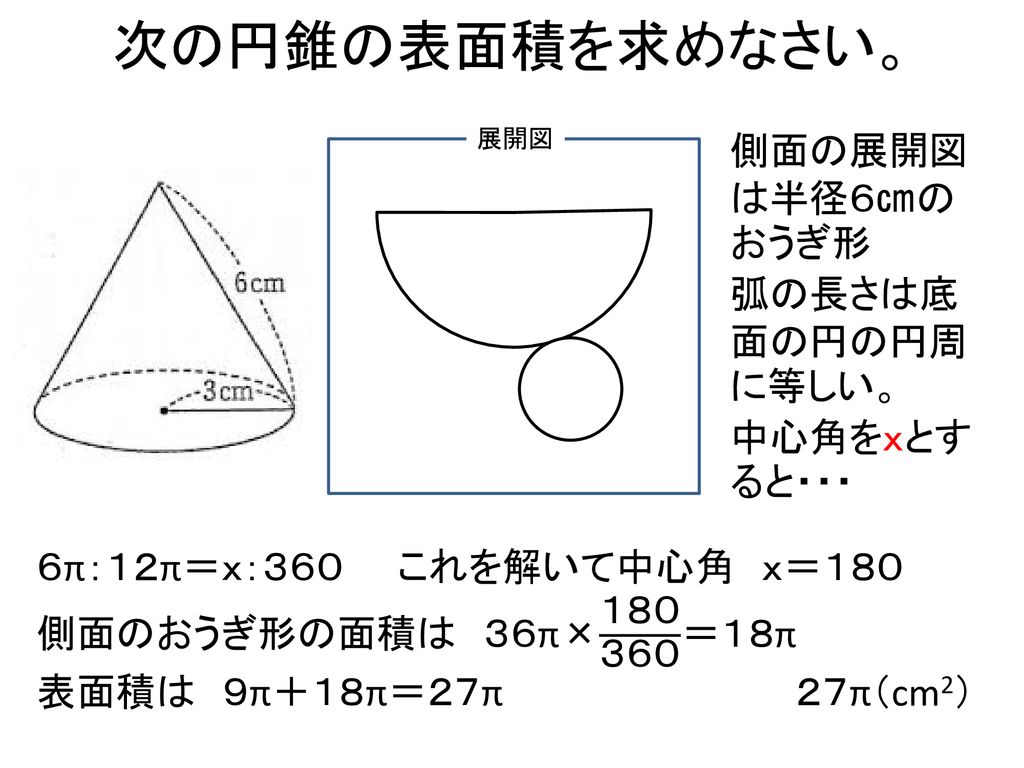


本時の目標 いろいろな立体の表面積を求めることができる Ppt Download



中1数学 円すいの問題 練習編 映像授業のtry It トライイット



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ


Coref U Tokyo Ac Jp Newcoref Wp Content Uploads 14 05 03soujnarittai Kyozai Pdf
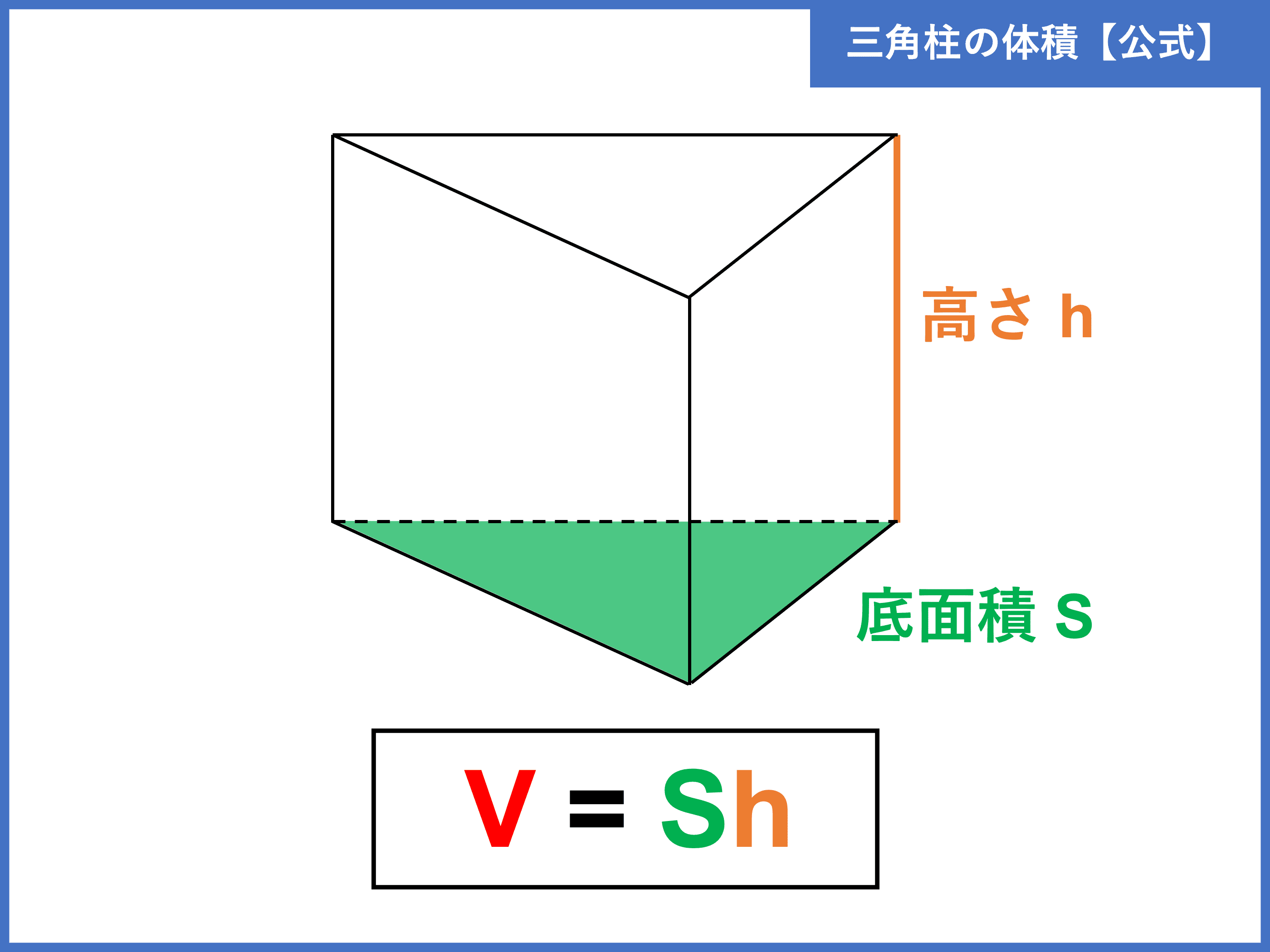


最高 50 三角柱 の 体積 公式 壁紙 配布
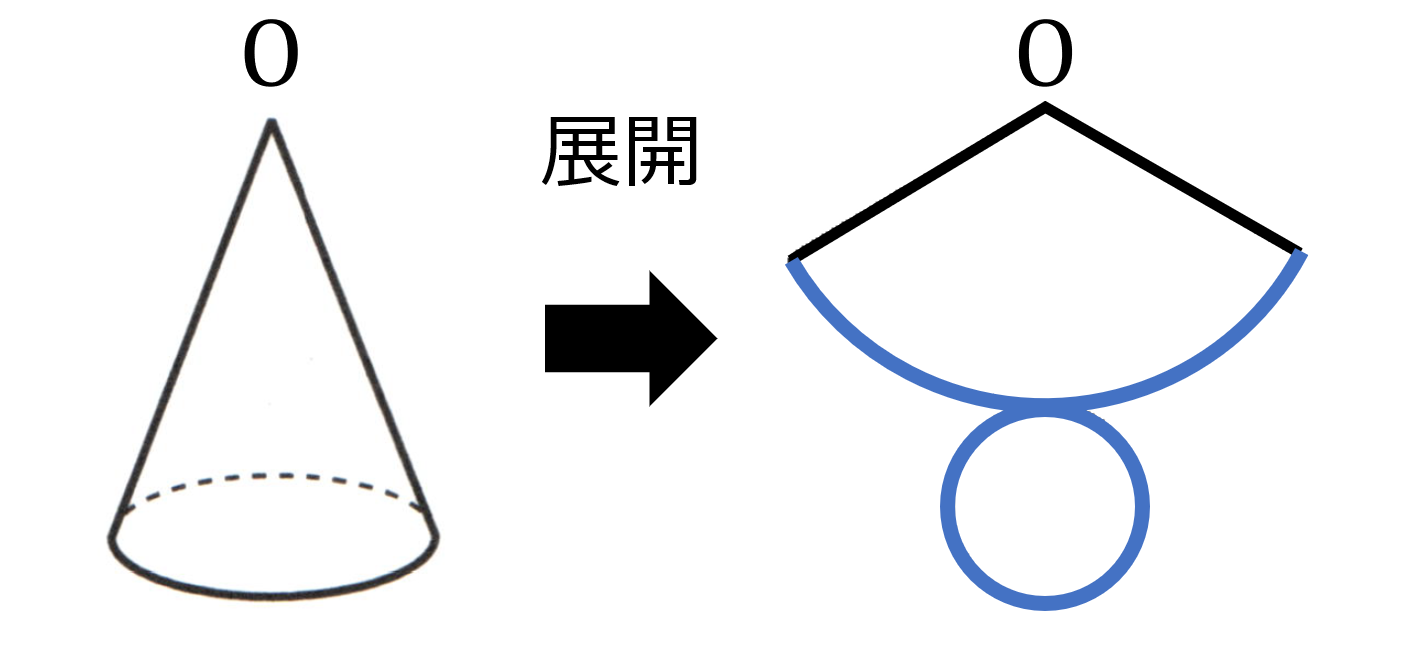


6章 空間図形 タカラゼミ



中1数学 円錐の表面積のポイント 中学生 数学のノート Clear



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学


Http Cms P01 Teacher Ne Jp Kamishizu Jh Library Suugaku 2nenprintimg Pdf
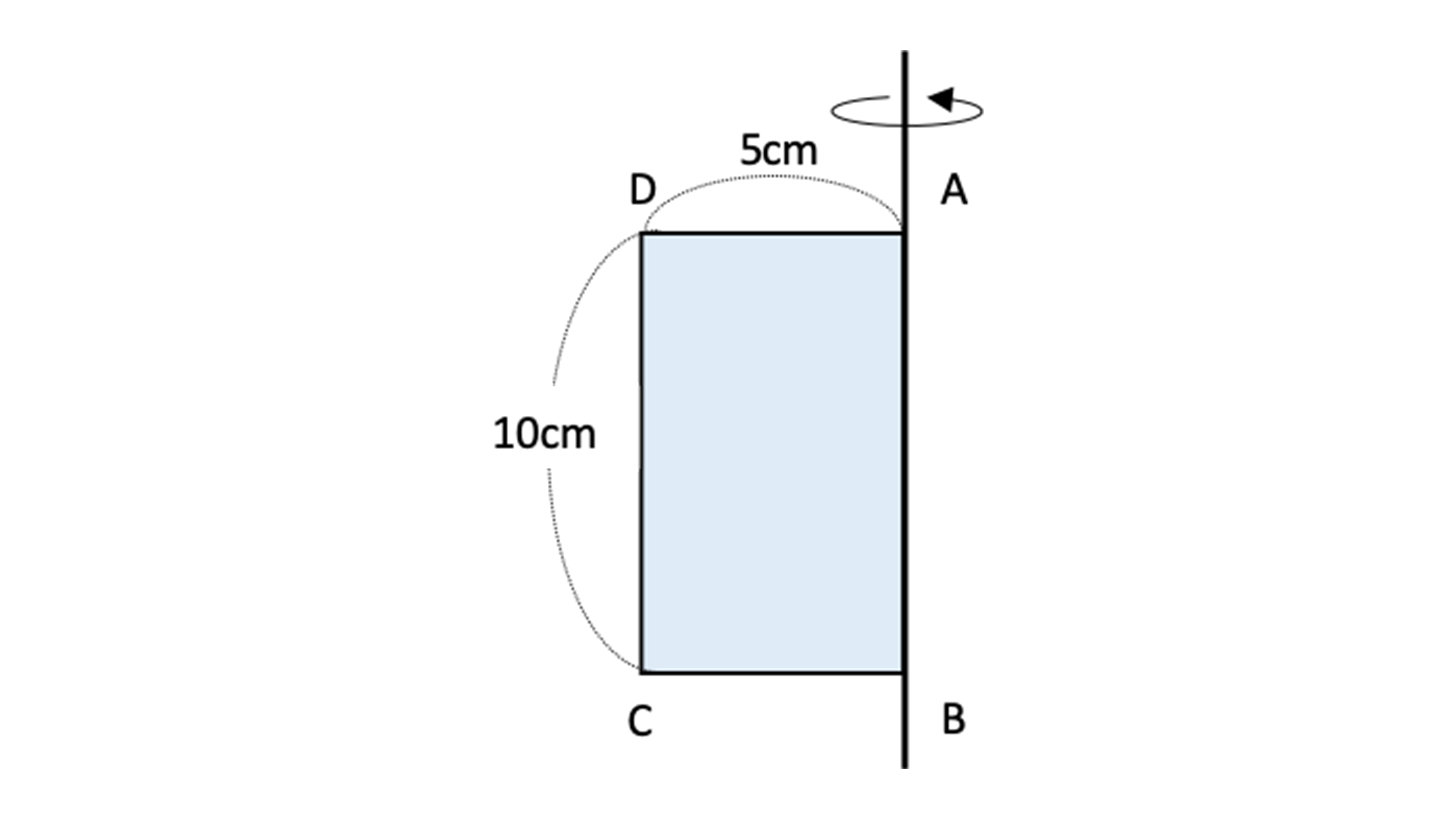


1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



三平方の定理の利用 四角錐 円錐 チーム エン
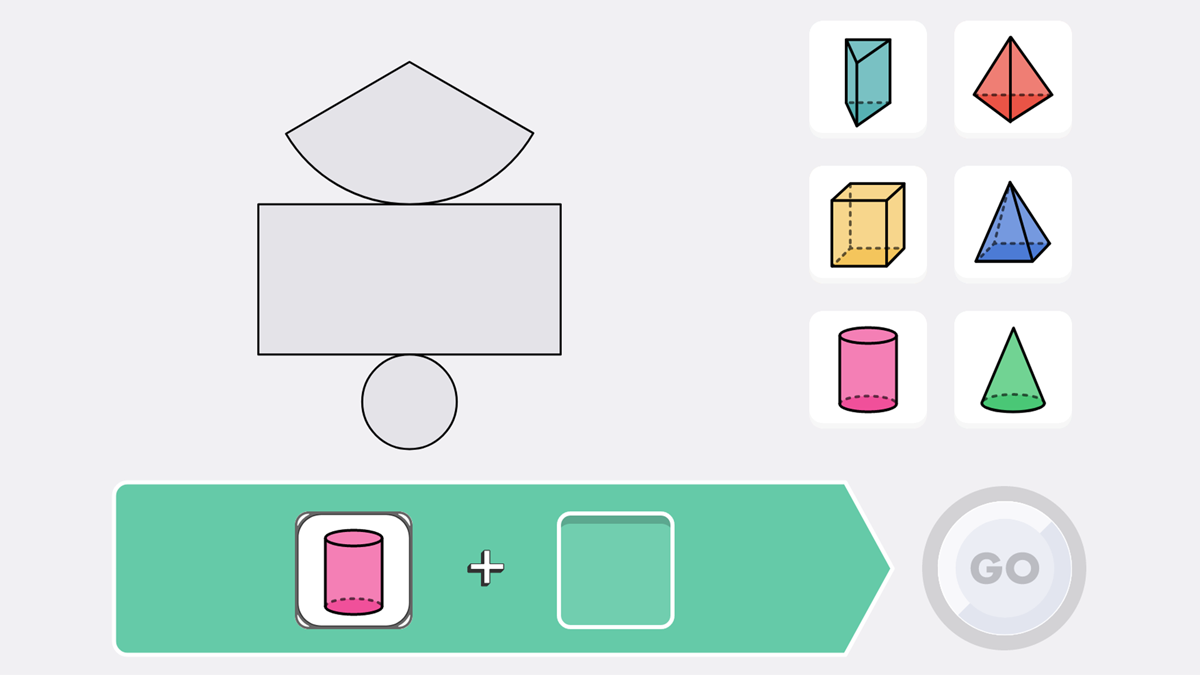


花まるラボ スマホやタブレットで使える中学受験対策アプリ 究極の立体 展開 を発売 Edtechzine エドテックジン


Http Www Edu C Pref Miyagi Jp Midori Gakuryoku Plan Pdf M Pdf 7nen M 7 06 Pdf



めっちゃ簡単 円錐の体積の求め方を解説 Tara Blog


Http Edu Fuku C Ed Jp Edudb Shidouandata H21 G45 Pdf
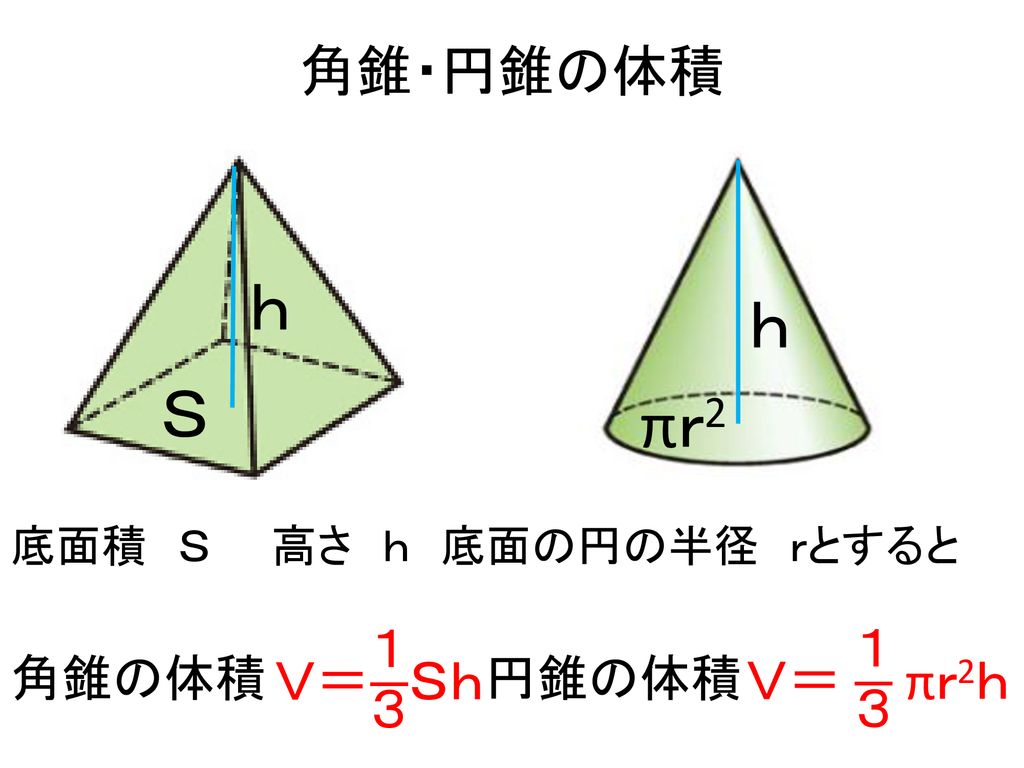


本時の目標 いろいろな立体の体積を求めることができる Ppt Download
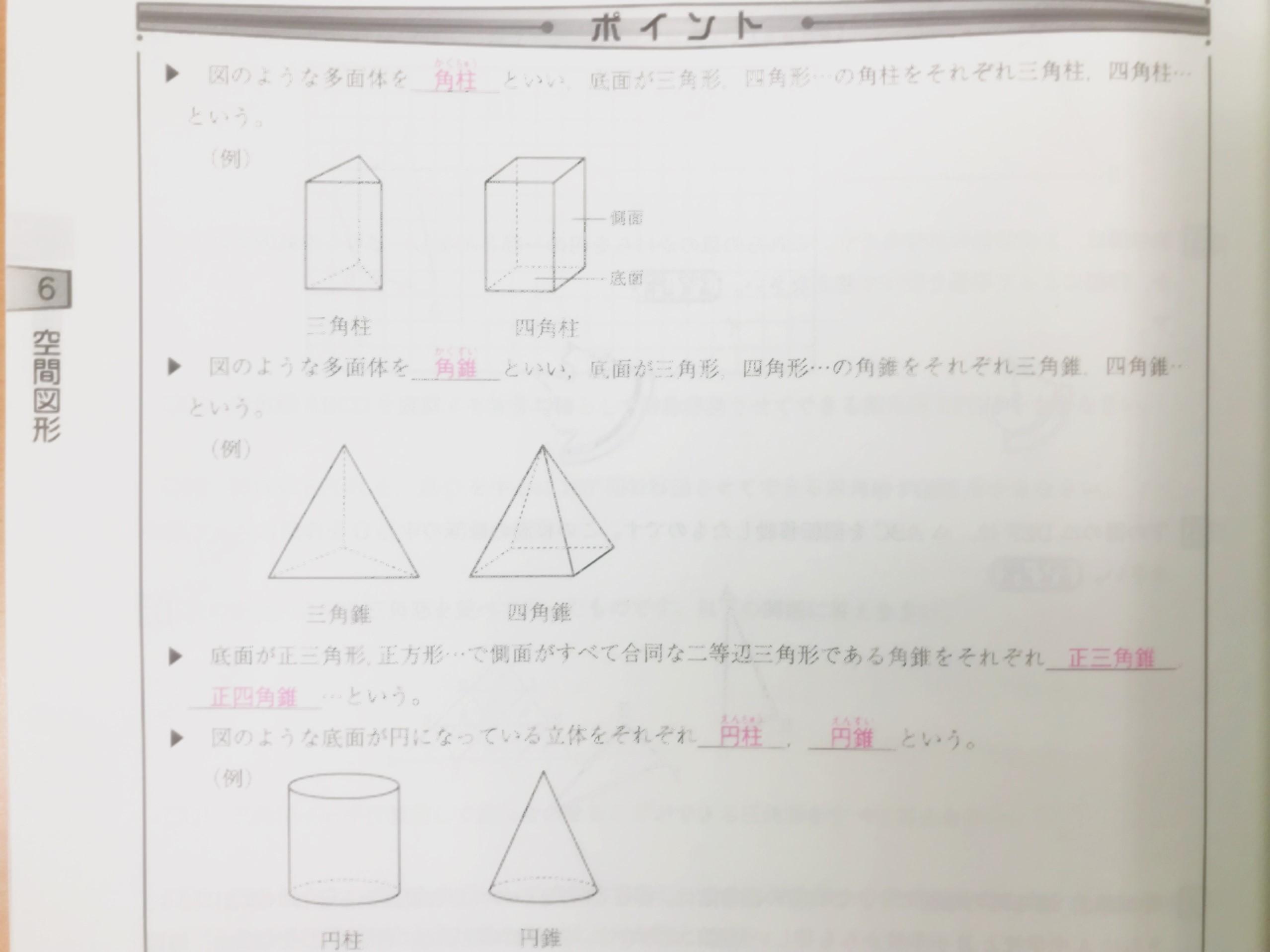


角柱 円柱 角錐 円錐の体積 滋賀県栗東市の個別塾 学習塾 ナビ個別指導学院 栗東校ブログ
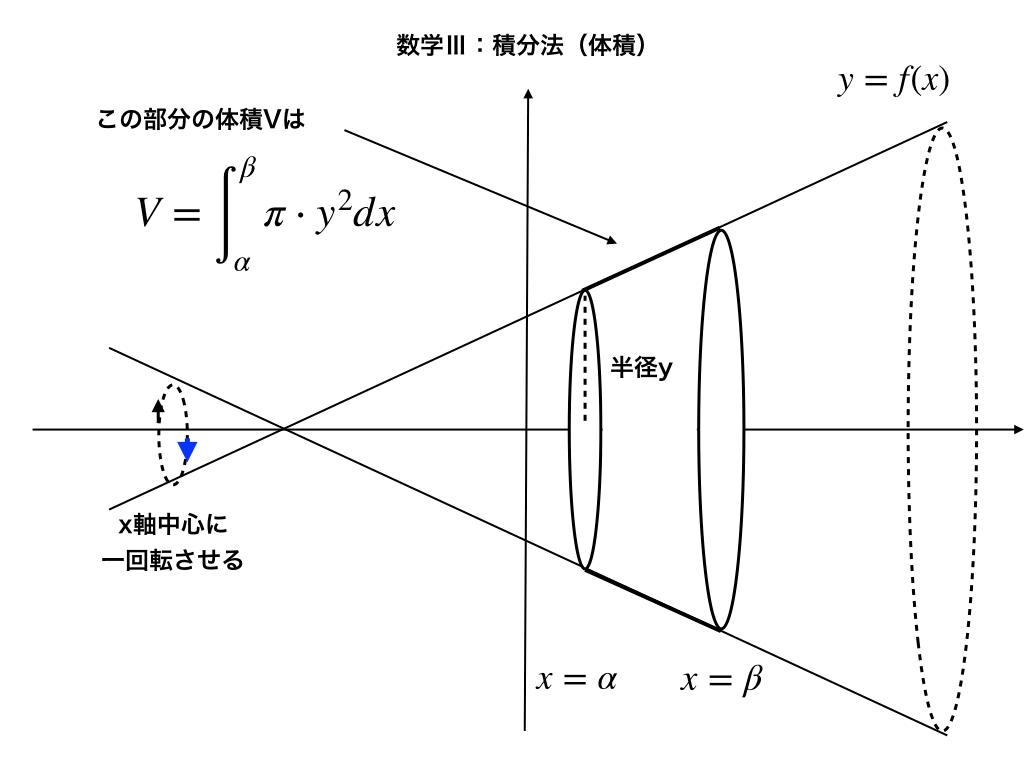


関数のグラフと接線が囲む面積 体積を求める問題をわかりやすく解説


数学 お前 まぁ やち ついてくぅだズ だば 円錐の体積の求め方 その2 ポンチャキー主夫の4コマ日記



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ


Http Edu Fuku C Ed Jp Edudb Shidouandata H21 G45 Pdf



マンスリーミニ対策 円錐台 中学受験プロ講師 コージー先生の独り言
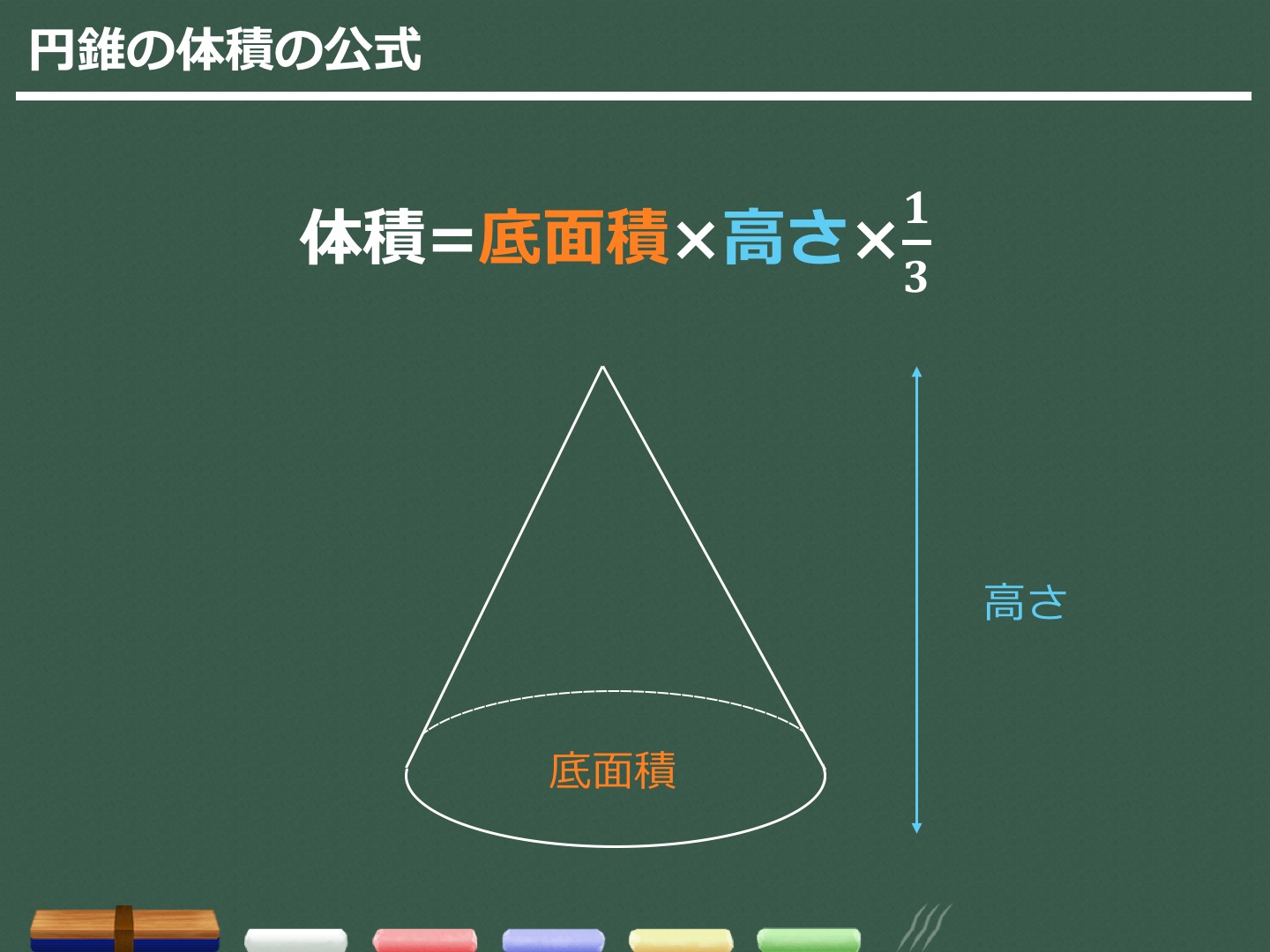


3分でわかる 円錐の体積 表面積の求め方 合格サプリ



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
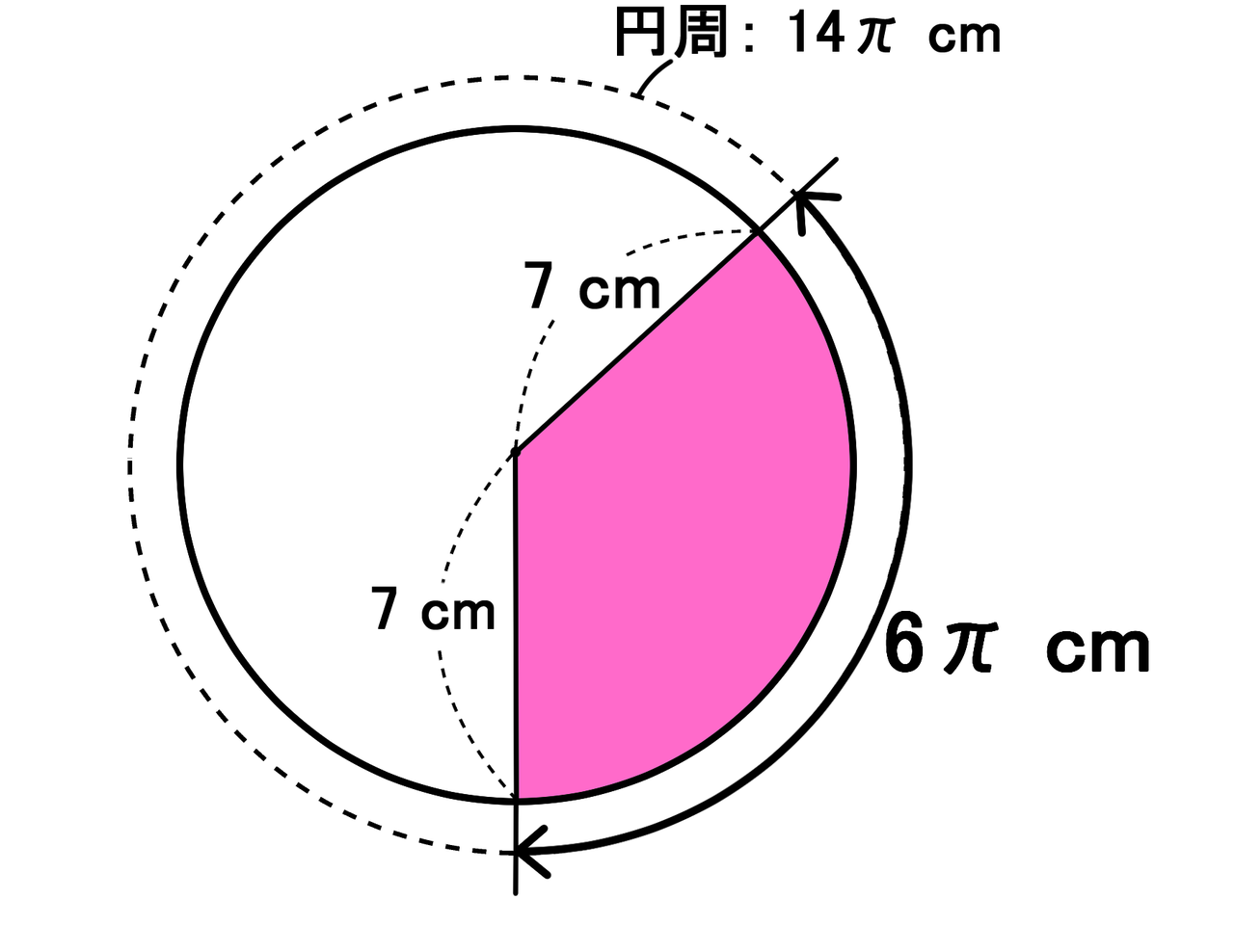


立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学


Core Ac Uk Download Pdf Pdf



四角錐 円錐の体積 チーム エン


